> # 03. 시계열분석 (Time Series Analysis)
>
> # 1. 차분 및 Box-Cox 변환
>
>
> data("AirPassengers")
> head(AirPassengers)
[1] 112 118 132 129 121 135
>
> par(mfrow=c(2,2))
> plot(AirPassengers, main = "Air Passengers")
> plot(diff(AirPassengers), main = "Difference - Air Passenger")
>
> library(forecast)
>
> lambda <- BoxCox.lambda(AirPassengers)
> lambda
[1] -0.2947156
> new <- BoxCox(AirPassengers, lambda)
>
> plot(new, main = "Box Cox - Air Passengers")
> plot(diff(new), main = "Diff./ Box Cox - Air Passengers")

> # 많은 시계열 자료는 차분을 수행하면 정상 시계열로 변환이 가능하다.
> # 그리고 시간에 따라 증폭하는 시계열 자료를 Box-Cox 변환을 하면 정상 시계열로 변환이 가능하다.
>
>
> # 3. 확률 모형
>
> # 1) AR 모형
>
> x=w=rnorm(300)
> for (t in 2:300) x[t]=0.7*x[t-1]+w[t]
> x.ts = ts(x)
>
> acf(x.ts, main = 'Yt=0.7*Yt-1+wt')
> pacf(x.ts, main = 'Yt=0.7Yt-1+wt')
>
> # 2) MA 모형
>
> x=w=rnorm(700)
> for (t in 2:700) x[t]=x[t]+0.7*w[t]
> x.ts = ts(x)
>
> acf(x.ts, main = 'Yt=at+0.7*at-1')
> pacf(x.ts, main = 'Yt=at+0.7*at-1')

>
> # 3) ARMA 모형
>
> par(mfrow=c(1,2))
> x=arima.sim(n=5000, list(ar=0.7,ma=0.2))
> x.ts = ts(x)
>
> acf(x.ts, main = 'Yt=0.7*Yt-1+at+0.2*at-1')
> pacf(x.ts, main = 'Yt=0.7*Yt-1+at+0.2*at-1')

>
> # 4) ARIMA 모형
>
> # ① ARIMA 자료 입력 및 정상성 검정(Nile dataset)
>
> dd <- Nile
> dd
Time Series:
Start = 1871
End = 1970
Frequency = 1
[1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020 960 1180 799 958 1140 1100 1210 1150
[24] 1250 1260 1220 1030 1100 774 840 874 694 940 833 701 916 692 1020 1050 969 831 726 456 824 702 1120
[47] 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759 781 865 845 944 984 897 822 1010 771
[70] 676 649 846 812 742 801 1040 860 874 848 890 744 749 838 1050 918 986 797 923 975 815 1020 906
[93] 901 1170 912 746 919 718 714 740
> summary(dd)
Min. 1st Qu. Median Mean 3rd Qu. Max.
456.0 798.5 893.5 919.4 1032.5 1370.0
> par(mfrow=c(1,1))
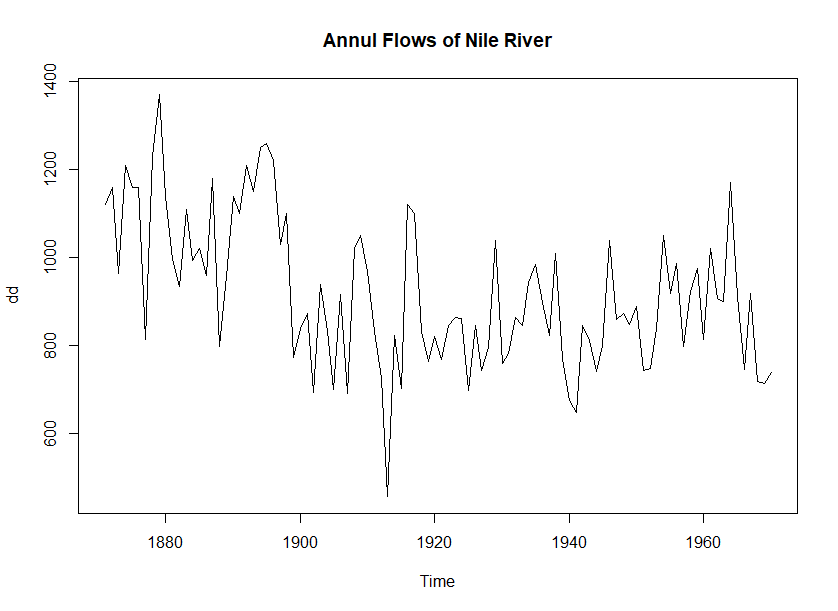
> plot(dd, main = 'Annul Flows of Nile River')
> par(mfrow=c(1,2)) ;acf(Nile);pacf(Nile)

>
> library(tseries)
> kpss.test(Nile)
KPSS Test for Level Stationarity
data: Nile
KPSS Level = 0.96543, Truncation lag parameter = 4, p-value = 0.01
경고메시지(들):
In kpss.test(Nile) : p-value smaller than printed p-value
> # 검정결과 유의확률 0.01 < 0.05, 비정상시계열로 판단된다.
>
> # ② 최적모형: auto.arima 적용한 결과 ARIMA(1,1,1) 설정
>
> am5 <- auto.arima(dd)
> summary(am5)
Series: dd
ARIMA(1,1,1)
Coefficients:
ar1 ma1
0.2544 -0.8741
s.e. 0.1194 0.0605
sigma^2 estimated as 20177: log likelihood=-630.63
AIC=1267.25 AICc=1267.51 BIC=1275.04
Training set error measures:
ME RMSE MAE MPE MAPE MASE ACF1
Training set -16.06603 139.8986 109.9998 -4.005967 12.78745 0.825499 -0.03228482
>
> # ③ 예측 결과
>
> forecast(am5)
Point Forecast Lo 80 Hi 80 Lo 95 Hi 95
1971 816.1813 634.1427 998.2199 537.7773 1094.585
1972 835.5596 640.8057 1030.3136 537.7091 1133.410
1973 840.4889 641.5646 1039.4132 536.2604 1144.717
1974 841.7428 640.0639 1043.4217 533.3015 1150.184
1975 842.0617 637.9589 1046.1645 529.9134 1154.210
1976 842.1429 635.7158 1048.5699 526.4399 1157.846
1977 842.1635 633.4558 1050.8712 522.9727 1161.354
1978 842.1687 631.2096 1053.1279 519.5345 1164.803
1979 842.1701 628.9843 1055.3558 516.1306 1168.210
1980 842.1704 626.7813 1057.5595 512.7613 1171.580
>
출처 : 2020 데이터 분석 전문가 ADP 필기 한 권으로 끝내기
'데이터분석 > R' 카테고리의 다른 글
| [ADP] 의사결정나무 (Decision Tree) (0) | 2022.01.15 |
|---|---|
| [ADP] 로지스틱 회귀분석 (Logistic Regression) (0) | 2022.01.15 |
| [ADP] 주성분분석(PCA, Principal Component Analysis) (0) | 2022.01.15 |
| [ADP] 정규화 모델 (0) | 2022.01.15 |
| [ADP] 그래프 작성 (0) | 2022.01.15 |



