> ### 4.2 중고차 특성의 차원 축소를 위한 데이터 분석 기법
>
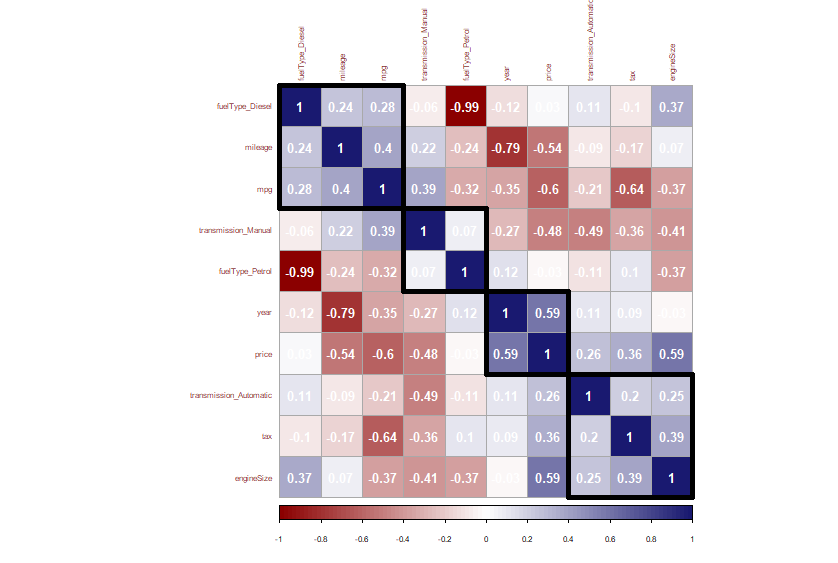
> # 상관행렬 그래프
> # 주성분분석은 예측자들의 공분산을 활용하기 때문에 일반적으로 상관계수가 높을수록 결과가 깔끔하게 나온다.
>
> library(corrplot)
> Corr_mat = cor(Audi2)
> corrplot(Corr_mat, method = "color", outline = T, addgrid.col = "darkgray",
+ order="hclust", addrect = 4, rect.col = "black",
+ rect.lwd = 5,cl.pos = "b", tl.col = "indianred4",
+ tl.cex = 0.5, cl.cex = 0.5, addCoef.col = "white",
+ number.digits = 2, number.cex = 0.8,
+ col = colorRampPalette(c("darkred","white","midnightblue"))(100))
>
> # 주성분 분석
>
> library(FactoMineR)
> Audi3 = as.data.frame(Audi2[1:100,])
> Principal_Component = PCA(Audi3,graph = FALSE)
> Principal_Component$eig
eigenvalue percentage of variance cumulative percentage of variance
comp 1 3.483151e+00 3.483151e+01 34.83151
comp 2 3.142647e+00 3.142647e+01 66.25798
comp 3 1.412029e+00 1.412029e+01 80.37827
comp 4 6.901200e-01 6.901200e+00 87.27947
comp 5 4.931755e-01 4.931755e+00 92.21122
comp 6 4.046871e-01 4.046871e+00 96.25809
comp 7 2.256980e-01 2.256980e+00 98.51507
comp 8 1.107700e-01 1.107700e+00 99.62277
comp 9 3.772260e-02 3.772260e-01 100.00000
comp 10 6.762775e-31 6.762775e-30 100.00000
> # 새로 생성된 축에 대한 정보를 출력한다.
> # eigenvalue : 고유값으로 생성된 주성분 중 몇 개의 주성분을 활용할지에 대한 지표로 활용
> # percentage of variance : 생성된 주성분이 원래 예측자들을 설명하는 비율
> # cumulative percentage of variance : 주성분의 누적 변동 설명 비율
> # 제 3성분까지의 누적 설명 비율은 80.37%이다.
>
> # Scree plot
> fviz_eig(Principal_Component, addlabels = TRUE, ylim = c(0, 50))

> # 주성분3까지 설명 비율이 큰 폭으로 감소한다.
>
> # 선형결합 확인
> Principal_Component$var$coord
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
year -0.41574569 0.4316897 0.65093358 -0.16403297 0.23409851
price 0.09959656 0.8454775 0.38541974 0.07313092 -0.19785289
mileage 0.52823573 -0.4565412 -0.43378509 0.29998631 0.15495828
tax 0.04476006 0.7801718 -0.08145093 0.34937178 0.45062570
mpg 0.22433848 -0.7936643 0.31141865 -0.34671982 0.17852058
engineSize 0.80207744 0.2236029 0.21136633 0.20587087 -0.33543542
transmission_Manual -0.61848601 -0.6161008 0.28087492 0.36274893 -0.02248080
transmission_Automatic 0.66283044 0.5013661 -0.37850451 -0.37350828 0.07528931
fuelType_Petrol -0.86712907 0.2382348 -0.37493210 -0.07784599 -0.10390288
fuelType_Diesel 0.86712907 -0.2382348 0.37493210 0.07784599 0.10390288
> # 주성분 선형결합의 해석에서 부호(+/-)는 크게 중요하지 않고 절대값의 크기가 중요하다.
>
> # 주성분 선형결합 시각화
> fviz_pca_var(Principal_Component, col.var="contrib",
+ gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
+ repel = TRUE # Avoid text overlapping
+ )

> fviz_pca_biplot(Principal_Component, repel = FALSE)

> # 같은 방향일수록 예측치의 상관성이 높은 것을 의미한다.
출처 : 실무 프로젝트로 배우는 데이터 분석 with R
'데이터분석 > R' 카테고리의 다른 글
| [실무 프로젝트로 배우는...] 마케팅의 RFM 분석 (0) | 2022.02.02 |
|---|---|
| [실무 프로젝트로 배우는...] 중고차 시세 확인 서비스 예측 분석 (0) | 2022.02.02 |
| [실무 프로젝트로 배우는...] 군집 분석 (0) | 2022.02.02 |
| [실무 프로젝트로 배우는...] 머신러닝 기초 (0) | 2022.01.31 |
| [실무 프로젝트로 배우는...] 분류 모형 (0) | 2022.01.31 |



