Section 01. 상관계수
> # 서로 다른 상관계수와 그에 따른 산점도의 변화
>
> set.seed(9)
> rvnorm <- function(r) {
+ x <- rnorm(50, 0, 1)
+ y <- rnorm(50, r*x, sqrt(1-r^2))
+ return(cbind(x,y))
+ }
>
> par(mfrow=c(1, 3), mar=c(2, 2, 2, 1), oma=c(0,0,0,0))
>
> r1 <- rvnorm(0.8)
> plot(r1, main="r=0.8")
> abline(lm(r1[,2] ~ r1[,1]), col="red")
>
> r2 <- rvnorm(0)
> plot(r2, main="r=0")
> abline(h=0, col="red")
>
> r3 <- rvnorm(-0.8)
> plot(r3, main="r=-0.8")
> abline(lm(r3[,2] ~ r3[,1]), col="red")

>
> ## 01) 아버지와 아들 키의 공분산과 상관계수
>
> hf <- read.table("https://www.randomservices.org/random/data/Galton.txt", header=T, stringsAsFactors = FALSE, sep = "\t")
> hf$Gender <- factor(hf$Gender, levels = c('M', 'F'))
>
> hf.son <- subset(hf, Gender == "M")
> hf.son <- hf.son[c("Father", "Height")]
>
> f.mean <- mean(hf.son$Father)
> s.mean <- mean(hf.son$Height)
> # 두 변수의 편차의 곱을 전부 합한 값
> cov.num <- sum((hf.son$Father - f.mean) * (hf.son$Height - s.mean))
> # 편차 곱의 합을 (자료의 개수-1)로 나눔
> (cov.xy <- cov.num / (nrow(hf.son) - 1))
[1] 2.368441
> # cov() 함수를 이용하여 표본공분산을 구한다.
> cov(hf.son$Father, hf.son$Height)
[1] 2.368441
> # 앞서 구한 값과 동일한 값임을 확인할 수 있다.
>
> # 직접 구한 표본공분산을 두 변수의 표본표준편차의 곲으로 나눈다.
> (r.xy <- cov.xy / (sd(hf.son$Father) * sd(hf.son$Height)))
[1] 0.3913174
> # cor() 함수를 이용하여 표본상관계수를 구한다.
> cor(hf.son$Father, hf.son$Height)
[1] 0.3913174
> # 앞서 구한 값과 동일한 값임을 확인할 수 있다.
>
> par(mfrow=c(1, 1), mar=c(4, 4, 1, 1))
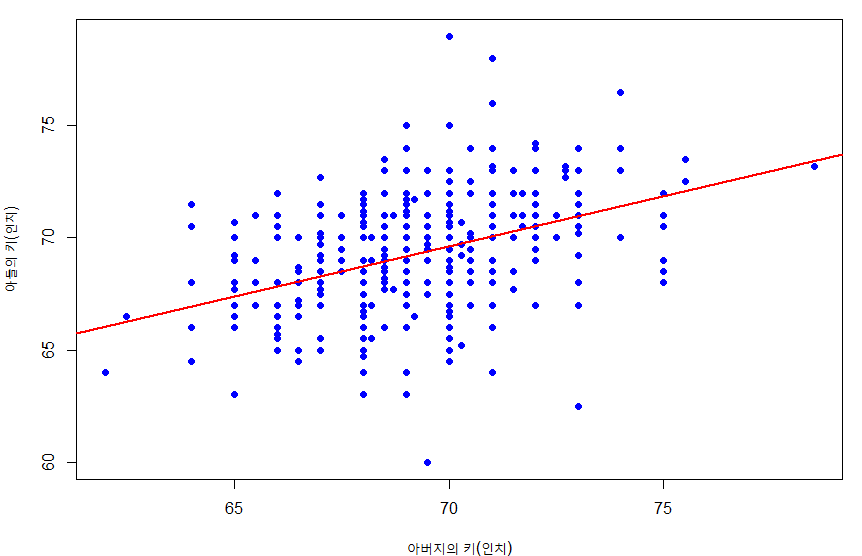
> plot(Height~Father, pch=16, data=hf.son, xlab="아버지의 키(인치)", ylab="아들의 키(인치)", col="blue")
> abline(lm(Height~Father, data=hf.son), col="red", lwd=2)
>
Section 02. 회귀분석
> # 2015년 서울의 미세먼지와 전국의 교통사고 발생건수
>
> pt <- read.csv("./data/pm10.traffic.accident.csv", header=T)
> cor(pt$pm10, pt$ta)
[1] -0.7441125
> library(ggplot2)
> ggplot(pt, aes(pm10, ta)) + geom_point(colour="blue", size=3) + theme_bw() + xlab("미세먼지(PM10)") + ylab("교통사고 발생건수")
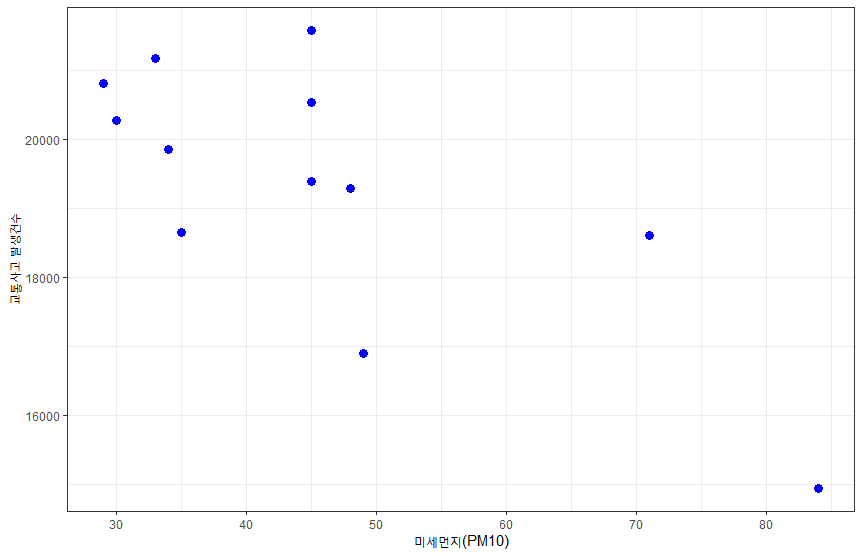
> # 두 변수의 상관관계는 적다고 할 수 있다.
>
> ## 02) 아버지와 아들 키 자료로부터 회귀계수 추정
>
> hf <- read.table("https://www.randomservices.org/random/data/Galton.txt", header=T, stringsAsFactors = FALSE, sep = "\t")
> hf$Gender <- factor(hf$Gender, levels = c('M', 'F'))
> hf.son <- subset(hf, Gender == "M")
> hf.son <- hf.son[c("Father", "Height")]
>
> mean.x <- mean(hf.son$Father)
> mean.y <- mean(hf.son$Height)
>
> # 편차 계산
> sxy <- sum((hf.son$Father - mean.x) * (hf.son$Height - mean.y))
> sxx <- sum((hf.son$Father - mean.x)^2)
>
> # 회귀계수들의 추정치 계산
> (b1 <- sxy / sxx)
[1] 0.4477479
> (b0 <- mean.y - b1 * mean.x)
[1] 38.25891
>
> # lm() 함수를 이용한 회귀계수 추정
> lm(Height ~ Father, data = hf.son)
Call:
lm(formula = Height ~ Father, data = hf.son)
Coefficients:
(Intercept) Father
38.2589 0.4477
> # 앞서 구한 값과 동일한 값임을 확인할 수 있다.
>
> # 총편차의 분해 (아버지와 아들의 키 부분 확대)
>
> hf <- read.table("https://www.randomservices.org/random/data/Galton.txt", header=T, stringsAsFactors = FALSE, sep = "\t")
> hf$Gender <- factor(hf$Gender, levels = c('M', 'F'))
> hf.son <- subset(hf, Gender == "M")
> hf.son <- hf.son[c("Father", "Height")]
>
> out <- lm(Height ~ Father, data=hf.son)
>
> mean.y <- mean(hf.son$Height)
>
> par(mar=c(4, 4, 1, 1))
> plot(Height~Father, pch=21, data=hf.son, xlim=c(75, 76), ylim=c(68, 75), xlab="아버지의 키(인치)", ylab="아들의 키(인치)")
> abline(h=mean.y, lwd=2, col="blue")
> abline(lm(Height~Father, data=hf.son), lty=3, col="green")
>
> lines(c(75.5, 75.5), c(mean.y, out$fitted.values[hf.son$Father==75.5][1]), col="orange")
> lines(c(75.5, 75.5), c(out$fitted.values[hf.son$Father==75.5][1], min(hf.son$Height[hf.son$Father==75.5])), lty=3, col="red", lwd=2)
>
> text(75.8, 70, expression(bar(y)))
> arrows(75.8, 69.7, 75.8, 69.3, length=0.08)
>
> text(75.8, 71, expression(hat(y)))
> arrows(75.8, 71.3, 75.8, 72, length=0.08)
>
> text(75.6, 70.5, expression(y-bar(y)))
> arrows(75.55, mean.y, 75.55, min(hf.son$Height[hf.son$Father==75.5]), angle=90, code=3, length=0.05, col="orange")
>
> text(75.4, 72.5, expression(y-hat(y)), col="red")
> arrows(75.45, out$fitted.values[hf.son$Father==75.5][1], 75.45, min(hf.son$Height[hf.son$Father==75.5]), angle=90, code=3, length=0.05, col="red", lty=3)
>
> text(75.4, 70, expression(hat(y)-bar(y)))
> arrows(75.45, out$fitted.values[hf.son$Father==75.5][1], 75.45, mean.y, angle=90, code=3, length=0.05, col="orange")

>
> ## 03) 회귀모형의 유의성 검정
>
> hf <- read.table("https://www.randomservices.org/random/data/Galton.txt", header=T, stringsAsFactors = FALSE, sep = "\t")
> hf$Gender <- factor(hf$Gender, levels = c('M', 'F'))
> hf.son <- subset(hf, Gender == "M")
> hf.son <- hf.son[c("Father", "Height")]
>
> out <- lm(Height ~ Father, data = hf.son)
> # 회귀의 분산분석표를 출력하고 검정통계량을 구한다.
> anova(out)
Analysis of Variance Table
Response: Height
Df Sum Sq Mean Sq F value Pr(>F)
Father 1 492.06 492.06 83.719 < 2.2e-16 ***
Residuals 463 2721.28 5.88
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> # 유의확률(p-value)이 거의 0에 가까워 회귀모형이 매우 유의함을 알 수 있다.
>
> ## 04) 회귀계수의 유의성 검정
>
> summary(out)
Call:
lm(formula = Height ~ Father, data = hf.son)
Residuals:
Min 1Q Median 3Q Max
-9.3774 -1.4968 0.0181 1.6375 9.3987
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 38.25891 3.38663 11.30 <2e-16 ***
Father 0.44775 0.04894 9.15 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.424 on 463 degrees of freedom
Multiple R-squared: 0.1531, Adjusted R-squared: 0.1513
F-statistic: 83.72 on 1 and 463 DF, p-value: < 2.2e-16
> # 각 회귀계수의 p-value가 0에 가까워 매우 유의함을 알 수 있다.
> # 수정된 결정계수(Adjusted R-squared)는 0.1513으로서 회귀모형이 나타내는 설명력이 부족함을 알 수 있다.
> # anova() 함수와 마찬가지로 F 통계량과 모형의 유의확률을 확인할 수 있다.
>
> # 아버지 키에 대한 아들의 키의 95% 신뢰구간
>
> no <- par(no.readonly = TRUE)
> par(mar=c(2,2,2,1))
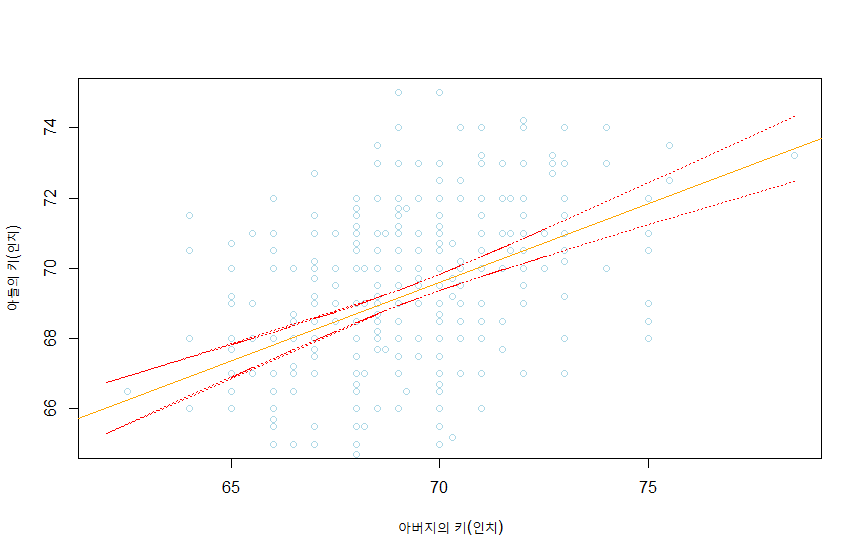
> plot(Height~Father, data=hf.son, main="", xlab="아버지의 키(인치)", ylab="아들의 키(인치)", ylim=c(65, 75), col="lightblue")
> abline(out, lwd=1.5, col="orange")
> ci <- predict(out, interval="confidence")
> lines(hf.son$Father, ci[,2], lty=3, lwd=1.5, col="red")
> lines(hf.son$Father, ci[,3], lty=3, lwd=1.5, col="red")
> par(no)
>
> # 잔차 분석을 통한 회귀분석의 가정 확인
>
> hf <- read.table("https://www.randomservices.org/random/data/Galton.txt", header=T, stringsAsFactors = FALSE, sep = "\t")
> hf$Gender <- factor(hf$Gender, levels = c('M', 'F'))
> hf.son <- subset(hf, Gender == "M")
> hf.son <- hf.son[c("Father", "Height")]
>
> out <- lm(Height ~ Father, data=hf.son)
> out2 <- lm(dist ~ speed, data=cars)
>
> # 잔차와 독립변수의 산점도 비교
> no <- par(no.readonly = TRUE)
> par(mfrow=c(1, 2), mar=c(2, 2, 2, 3))
> plot( hf.son$Father, residuals(out), xlab="residuals", ylab="", col="lightblue")
> abline(h=0, col="red", lty=2)
> plot( cars$speed, residuals(out2), xlab="residuals", ylab="", col="lightblue")
> abline(h=0, col="red", lty=2)
> par( no )
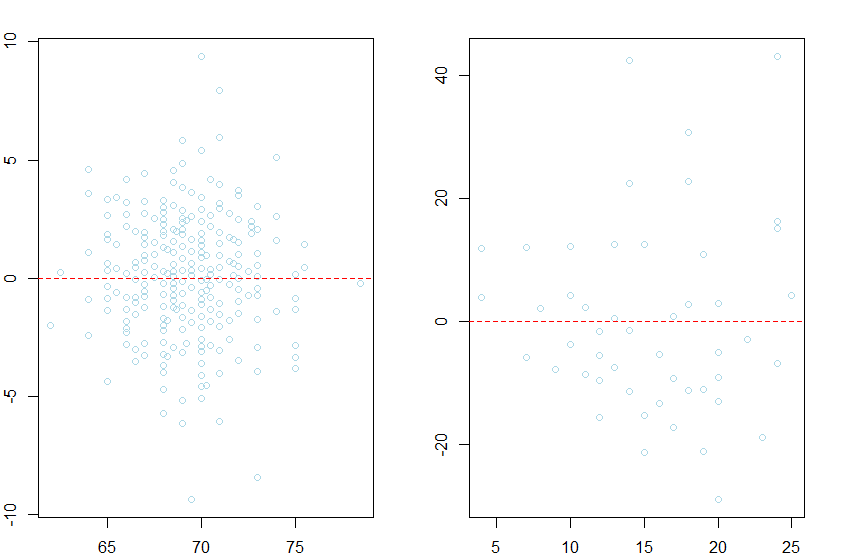
> # 잔차들이 서로 등분산일 경우, 잔차와 예측값의 산점도가 첫번째 그림처럼 랜덤하게 0 주변에 몰려있게 된다.
>
> # 정규확률그림 비교
> no <- par(no.readonly = TRUE)
> par(mfrow=c(1, 2), mar=c(2, 2, 2, 3))
> qqnorm(residuals(out), main="", col="lightblue")
> qqline(residuals(out), lty=2, col="red")
> qqnorm(residuals(out2), main="", col="lightblue")
> qqline(residuals(out2), lty=2, col="red")
> par( no )
> # 첫번째 그림에서는 붉은 점선으로 나타나는 정규분포의 적합선 위에 잔차가 고르게 분포해 있는 경향이 강하나 ±3 근처에서 조금 벌어지고 있다.
> # 두번째 그림에서는 적합선에서 다소 떨어져 있는 형태를 보이고 있어 정규분포가 의심스러운 상황이다.
>
> # 정규성 검정
> shapiro.test(residuals(out2))
Shapiro-Wilk normality test
data: residuals(out2)
W = 0.94509, p-value = 0.02152
> # 유의확률(p-value)이 0.02152로 유의수준 0.05보다 작아 잔차들은 정규분포를 따르지 않는 것으로 판단된다.
출처 : 이윤환, ⌜제대로 알고 쓰는 R 통계분석⌟, 한빛아카데미, 2020
'데이터분석 > R' 카테고리의 다른 글
| [R 통계분석] 범주형 자료분석 (0) | 2022.08.19 |
|---|---|
| [R 통계분석] 여러 모집단의 평균 비교 검정 (0) | 2022.08.15 |
| [R 통계분석] 가설검정 (0) | 2022.08.12 |
| [R 통계분석] 추정 (0) | 2022.08.11 |
| [R 통계분석] 표본분포 (0) | 2022.08.10 |



